三葉草之家: 2018

2018年11月21日星期三

iTerm2 顯示/輸入中文

輸入中文:
1.編輯~/.inputrc
set convert-meta off
set meta-flag on
set output-meta on

輸入unicode中文:
1.編輯 ~/.vimrc
set env=utf8

延續上
set fileencodings=utf8,big5
set encoding=utf8
set tenc=utf8

2018年10月10日星期三

Linux安裝套件出現“has no installation candidate”解決方式

編輯套件來源檔:
sudo vim /etc/apt/sources.list

加入下面來源位址:

deb http://archive.ubuntu.com/ubuntu/ trusty main restricted universe multiverse 
deb http://archive.ubuntu.com/ubuntu/ trusty-security main restricted universe multiverse 
deb http://archive.ubuntu.com/ubuntu/ trusty-updates main restricted universe multiverse 
deb http://archive.ubuntu.com/ubuntu/ trusty-proposed main restricted universe multiverse 
deb http://archive.ubuntu.com/ubuntu/ trusty-backports main restricted universe multiverse

再執行一次update:

sudo apt-get update

2018年9月23日星期日

Virtual box guest additions: modprobe vboxsf failed

Ubuntu 無法安裝 VirtualBox Guest Additions 出現下面訊息:
Virtual box guest additions: modprobe vboxsf failed
解決方式:

1. 開啟終端機輸入
sudo apt-get install dkms build-essential linux-headers-$(uname -r)

2. reboot

3. 掛載 VirtualBox Guest Additions imageCD

4. cd /media/<username>/VBox_GAs_5.2.18

5. sudo ./VBoxLinuxAdditions.run

或是:

1. 開啟終端機輸入 sudo apt-get install virtualbox-guest-dkms

2. sudo apt-get install linux-headers-virtual

3. 重新開機

4. 掛載 VirtualBox Guest Additions imageCD

5. cd /media/<username>/VBox_GAs_5.2.18

6. sudo ./VBoxLinuxAdditions.run

2018年7月14日星期六

真露燒酒

有時看著韓劇裡喝著燒酒也想買瓶來喝，剛好有親戚去韓國旅遊就順便託她帶了2瓶回來。
原本以為燒酒會有米酒的味道，其實不然，冰過之後的燒酒搭配燒烤還蠻好喝的。
只是這精濃度有16.9%還是不可小覷啊。

2018年6月25日星期一

我的西貢時光-越南滴滴壺

越南壺何時、何人發明已不可考，一般相信是1859年起法國殖民越南時期，在越南用越南壺放入焦黑出油的越式咖啡粉，濾出後的黑苦咖啡 + 煉奶攪勻後飲用。

越南咖啡之所以別具風情，在於它的沖泡過程完全不經電力或機械，只需一個簡易的滴滴壺就能製作出道地的越南咖啡。滴滴壺的好處是一次一杯，比例與時間容易控制，攜帶、收納、清洗非常方便；缺點是篩孔較大，滴餾時難免會有微量的咖啡渣飄浮其中。越式滴滴壺分成鋁製與不鏽鋼製兩種，配件包含：篩子、壺身、蓋子三部分。

越南當地較為盛行的咖啡是咖啡加入煉乳的，因為傳統越南咖啡的味道相當苦澀，所以越南人發明了加入煉乳的飲用方式，聽說很多越南人不管早中晚都在喝咖啡，只要有這簡單的滴壺就能夠悠閒地享用咖啡。

首先準備：
A．中度或是深度烘培，中等顆粒咖啡粉，喝起來會更道地，越南咖啡的口味是非常重的。您也可自行研磨咖啡豆，記得磨成中等粗細，避免滴餾時殘留太多咖啡渣。
B．越式滴滴壺（我使用不鏽鋼製、直徑6 cm的最小尺寸）。
C．煉乳(鮮奶、奶精都可以)。
D．正方體冰塊，咖啡在先熱後冷的交替作用下就能散發極致的風味。
E．一高一矮透明玻璃杯。
F．90℃的熱水 (煮沸的礦泉水更好)。

沖泡過程如下：
1．放入1匙的咖啡粉 (約10g~12g)，輕拍壺身使咖啡粉均勻分佈。

2．注入少許熱水"悶蒸" (約20ml)，等30秒左右讓咖啡粉充分吸水膨脹。
※註:"悶蒸"是製作手泡咖啡過程中十分重要的一個環節。好的悶蒸能夠使咖啡粉充分浸潤，刺激咖啡活性，水量就控制在咖啡粉的等重至2倍水量即可。

3．把篩子壓板往下壓實 (不可太緊或太鬆，鬆或緊的力道要多做幾次才能掌握)，再注入5、6分滿的熱水 (約50、60ml)，蓋上蓋子保溫。理想情況下，咖啡會在5、6分鐘內滴完。這個過程很關鍵，若滴得太快或太慢，表示水粉比例、篩子鬆緊或濾泡溫度出了問題，可能導致咖啡太淡、偏苦、或提早變冷 (要多練習幾次吧)。

4．在高的透明玻璃杯放滿冰塊與煉乳，然後將滴滴壺的蓋子翻過來盛著滴滴壺 (咖啡就不會滴出來)，再把矮玻璃杯裡的咖啡倒入高玻璃杯攪拌，最後再等個30秒讓咖啡、煉乳與冰塊徹底融合，即可享用別具風味的越南咖啡。

2018年6月4日星期一

LISP Programming 1062_ex9

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 9: enumerating tuples
•Define a procedure, (enum-tuples list-1 list-2 .... list-k) which will
generate a list of k-tuples. The tuples contains all combinations of
elements from each list.

$ scheme48
> ,load ex9-enum-tuples.scm
> 
> (enum-tuples)
()
> (enum-tuples '(x y z))
((x) (y) (z))
> (enum-tuples '(a b c) '(hello world))
((a hello) (b hello) (c hello) (a world) (b world) (c world))
> (enum-tuples '(1 2) '(h i j k))
((1 h) (2 h) (1 i) (2 i) (1 j) (2 j) (1 k) (2 k))
> (enum-tuples '(hello ohio) '(101 39 11) '(good fine))  
((hello 101 good) (ohio 101 good) (hello 39 good) (ohio 39 good)
(hello 11 good) (ohio 11 good) (hello 101 fine) (ohio 101 fine)
(hello 39 fine) (ohio 39 fine) (hello 11 fine) (ohio 11 fine))
> ,exit
$

解答:

;exer9 enumerating tuples
(define proc-list
    (lambda (lst f)
        (cond
            ((null? lst) '())
            (else
            (append (f (car lst)) (proc-list (cdr lst) f)))))
) ;proc-list END
(define combine
  (lambda (list1 list2)
    (proc-list list1 (lambda (x)
                     (map (lambda (y) (list x y)) list2))))
) ;combine END
(define enum-tuples
  (lambda (x-lst . y-lst*)
    (cond
      ((null? y-lst*) (map list x-lst)) ;case1: (enum-tuples '(x y z))
      ((null? (cdr y-lst*)) (combine x-lst (car y-lst*)))
      (else
          (proc-list x-lst (lambda (x)
                           (map (lambda (y) (cons x y))
                                (apply enum-tuples y-lst*)))))))
) ;enum-tuples END

執行結果：

2018年5月28日星期一

LISP Programming 1062_ex8

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 8: enumerate a tree with sequence interface
•Rewrite (enum-tree T) with accumulate and map.

解答:

;enumerate tree
(define (enumerate-tree tree)
  (cond ((null? tree) '())
        ((not (pair? tree))
              (list tree))
        (else (append (enumerate-tree (car tree))
                      (enumerate-tree (cdr tree))))))
;use map list a tree to see ex2.30
;(1) map a tree
(define (lst x) (append x))
(define (map-tree t)
    (enumerate-tree
        (map (lambda (sub-tree)
             (if (pair? sub-tree)
                 (map-tree sub-tree)
                 (lst sub-tree)))
                t)))
(define nil '())

;p78 accumulate.scm
(define (accumulate op initial sequence)
    (if (null? sequence)
        initial
        (op (car sequence)
            (accumulate op initial (cdr sequence))))
)
;(2) accumulate a tree
(define (enum-tree t )
   (accumulate cons
               (list)         ;empty list
               (map-tree t)))

執行結果：

2018年5月21日星期一

LISP Programming 1062_ex7

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 7: mapping over trees
•Refer to exercise 2.31.

解答:

(define l (list 1 (list 2 3 (list 4 5))))

(define (sq x) (* x x))

(define (tree-map f tree)
  (cond ((null? tree)
          '())
        ((not (pair? tree))
          (f tree))
        (else
          (cons (tree-map f (car tree))
                (tree-map f (cdr tree))))))

執行結果：

2018年5月7日星期一

LISP Programming 1062_ex6

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 6: representing a pair with a number
•Refer to exercise 2.5.
•Note the requirement of nonnegative is removed. Your method 
should accept two integers.

解答:

(define (num-cons a b)
    (* (expt 2 a) (expt 3 b)))

(define (num-car n)
  (if (= 0 (modulo n 2))
      (+ 1 (num-car (/ n 2)))
      0))

(define (num-cdr n)
  (if (= 0 (modulo n 3))
      (+ 1 (num-cdr (/ n 3)))
      0))

執行結果：

2018年4月30日星期一

LISP Programming 1062_ex5

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 5: calculating continued-fraction
•Refer to exercise 1.37.(參考這篇：黃金分割)
•You have to write two procedures. One is (cont-frac n d k) and another is (pi epsilon).
•The "cont-frac" should be implemented in linear iterative way.
•To calculate pi, the sequence N_i is: 4, 1^2, 2^2, 3^2, ...
and the sequence D_i is: 1, 3, 5, 7, ...
•To approximate pi, calculate (cont-frac n d 1), (cont-fract n d 2), .. until two consecutive values
are close enough, that is, the distance between them is less than epsilon.

$ scheme48
> ,load ex5.scm
> (cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 100)
0.6180339887498948
> (pi 0.001)
3.141463414634146
> (pi 0.0001)
3.1415888250921244
> (pi 0.0000000000001)
3.141592653589791
> ,exit
$
解答說明請參考：【Scheme】連分法求pi

解答:

;continued fraction calc pi
(define (cont-frac n d k)
   (define (frac-iter i result)
       (if (= i 0)
           result
           (frac-iter (- i 1.0) (/ (n i) (+ (d i) result)))))
   (frac-iter (- k 1.0) (/ (n k) (d k))))
(define (calc-pi k)
    (define (d i)
        (- (* 2 i) 1))
    (define (n i)
        (if (= i 1)
            4
            (* (- i 1) (- i 1))))
    (cont-frac n d k))
(define (calc-enough index accuracy)
    (define next_i index) ;next_i=index
    (if (< (abs (- (calc-pi index) (calc-pi (+ next_i 1)))) accuracy)
        (calc-pi (+ next_i 1))               ;true
        (calc-enough (+ index 1) accuracy))) ;false
(define (pi accuracy)
    (calc-enough 1 accuracy))

執行結果：

【Scheme】連分法求Pi

題目要求:
•Refer to exercise 1.37.
•You have to write two procedures. One is (cont-frac n d k) and another is (pi epsilon).
•The "cont-frac" should be implemented in linear iterative way.
•To calculate pi, the sequence N_i is: 4, 1^2, 2^2, 3^2, ...
and the sequence D_i is: 1, 3, 5, 7, ...
•To approximate pi, calculate (cont-frac n d 1), (cont-fract n d 2), .. until two consecutive values
are close enough, that is, the distance between them is less than epsilon.

參考SICP ex 1.37，寫兩個程序
1. (cont-frac n d k) and (pi epsilon)
2. "cont-frac" 使用迭代法
3. 計算 Pi，序列N_i 是4，1^2，2^2，3^2 . . .D_i是 1，3，5，7 . . .
4. 近似求Pi，直到(cont-frac n d 1), (cont-fract n d 2)值小於精確值

首先 π 的連分公式如下:

其中4,1,4,9,16就是N_i 項; 而 1,3,5,7,9就是Ｄ_i項,
參考上一篇的(cont-frac)，迭代法程式:

(define (cont-frac-iter n d k)
   (define (frac-iter i result)
       (if (= i 0)
           result
           (frac-iter (- i 1) (/ (n i) (+ (d i) result)))))
   (frac-iter (- k 1) (/ (n k) (d k))))

接著解釋 n項與 d項:
這裡要注意的是
d項就是迭代 i值的(2*i-1)，例如第一項是(2*1-1)=1，第二項是(2*2-1)=3 . . .依此類推
而n項就是迭代 i值的平方(i^2)，但要注意第一項是4，第二項是((2-1)^2)，第三項是((3-1)^2) . . .

(define (calc-pi k)
    (define (d i)
        (- (* 2 i) 1)) ;((2*i)-1)
    (define (n i)
        (if (= i 1)
            4
            (* (- i 1) (- i 1))))
    (cont-frac n d k))

這樣就可以求Pi，例如(calc-pi 10)，求出聯分法10項的Pi值:
(calc-pi 10)
3.14159254044654
(calc-pi 20)
3.14159265358979
用這種方式求Pi因為收斂很快所以不會花費太多時間。

接著要給精確值求出Pi，就是用迭代法每一次求出的Pi值與下一個項次比較，直到小於精確值為止
如:
(calc-pi 5)-(calc 6) < accuracy ?
如果是則停止
如果不是則(calc-pi 6)-(calc-pi 7)

(define (inc x)
    (+ x 1))
(define (enough-pi index accuracy)
    (define next_i index) ;next_i=index
    (if (< (abs (- (calc-pi index) (calc-pi (inc next_i)))) accuracy)
        (calc-pi (inc next_i))            ;true
        (enough-pi (inc index) accuracy)) ;false
)
(define (pi accuracy)
    (enough-pi 1 accuracy))

輸入與結果:
(pi 0.001)
3.14146341463415
(pi 0.0001)
3.14158882509212
(pi 0.0000000000001)
3.14159265358979
如果將各項的輸出印出

index:5 next_i:5 err:0.001
3.14146341463415
在第5項的時候收斂到0.001

index:7 next_i:7 err:0.0001
3.14158882509212
在第7項的時候收斂到0.0001

index:19 next_i:19 err:1e-13
3.14159265358979
在第19項的時候收斂到0.0000000000001

參考:
1.維基百科圓周率
2. SICP Ex 1.37

2018年4月22日星期日

【Scheme】SICP Ex.1.37

Exercise 1.37. a. An infinite continued fraction is an expression of the form
在SICP練習1.37 中要求寫出連分法的表示，公式如下:

而這個除法式可以用一個遞迴表達式來表示如下：

其中函數 cf(i) 表示連分式的第 i 個項。

因此Scheme程式遞迴寫法如下:

(define (cont-frac n d k)
  (define (frac i)
     (if (< i k)
         (/ (n i) (+ (d i) (frac (+ i 1))))
         (/ (n i) (d i))))
  (frac 1))

迭代寫法如下:

(define (cont-frac-iter n d k)
   (define (frac-iter i result)
       (if (= i 0)
           result
           (frac-iter (- i 1) (/ (n i) (+ (d i) result)))))
   (frac-iter (- k 1) (/ (n k) (d k))))

可以用下面的近似驗證:

> (cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 100)0.618033988749895

這就是黃金分割比例值。

參考:
1. SCIP 教材

2018年3月26日星期一

LISP Programming 1062_ex3

http://erdos.csie.ncnu.edu.tw/~klim/scheme/lisp-1062.html

exercise 3: linear recursive and linear iterative
Refer to exercise 1.11 but the formula is changed to
  f(n) = n if n < 3
  f(n) = 2*f(n-1) + f(n-2) + f(n-3) if n ≥ 3 and n is even
  f(n) = 2*f(n-1) - f(n-2) + f(n-3) if n ≥ 3 and n is odd
Note that you have to write two procedures. One is written
in recursive way and another in linear iterative way.

解答:

;f by means of a recursive process
(define (f-res n)
    (if (< n 3)
        n  ; n<3 , f(n)=n
        (if (odd? n)
            (+ (- (* 2 (f-res (- n 1))) 
               (f-res (- n 2))) 
            (f-res (- n 3))) ; n is odd
            
            (+ (+ (* 2 (f-res (- n 1))) 
               (f-res (- n 2))) 
            (f-res (- n 3)))))) ; n is even
(define (f n)
    (f-res n))

執行結果：

2018年3月22日星期四

無法連接iCloud解決方法

這幾天Mac開機後會出現"無法連接iCloud"訊息(如上圖)並導引到系統偏好設定去輸入密碼，解決的方式如下:

1. 開啟系統偏好，點選iCloud。

2. 點選帳號詳細資訊。

3. 點選安全性，然後下面有開啟雙重驗證，點選後要求輸入電話號碼，之後會傳驗證碼簡訊到手機，將驗證碼輸入即可。

參考資料:
Apple Support

2018年3月21日星期三

Ubuntu 16.04 R語言安裝

唸數學系的兒子這學期有修R語言，雖然系上有在上學期末短暫的教導用VirtualBox安裝Ubuntu，不過對於初接觸Linux的人來說還是太生疏了。R語言是統計分析的利器，目前是開源可以安裝在Windows，Linux，MacOSX等作業系統，這邊我用Linux 的Ubuntu 16.04 來講解R語言安裝方式及IDE的安裝方式。

1. 安裝R:
安裝R語言可以在Ubuntu環境下使用終端機下:

$ sudo apt-get install r-base

來安裝是最簡便的，安裝完成後在終端機輸入R即可執行。

如果需要IDE整合環境就必須安裝RStudio

2.安裝R Studio:

先到官網下載安裝包:

https://www.rstudio.com/products/rstudio/download/#download

Ubuntu 對應的檔案是 RStudio 1.1.442 - Ubuntu 12.04-15.10/Debian 8 (64-bit) 這個壓縮檔。

下載後解壓縮:

$tar -zxvf rstudio-1.0.136-amd64-debian.tar.gz

接著cd rstudio-1.0.136/bin 目錄下執行 ./rstudio

會出現下面的訊息:

rstudio: error while loading shared libraries: libgstreamer-0.10.so.0: cannot open shared object file: No such file or directory

原因是缺少libgstreamer-0.10.so.0和libgstapp-0.10.so.0

可用apt-file命令來尋找缺少的檔案

Ubuntu內定是沒有安裝apt-file的，所以要先安裝

$sudo apt-get install apt-file
$sudo apt-file update

接著用 apt-file 尋找 libgstreamer-0.10.so.0 所對應的文件

$apt-file search libgstreamer-0.10.so.0

libgstreamer0.10-0: /usr/lib/x86_64-linux-gnu/libgstreamer-0.10.so.0  

libgstreamer0.10-0: /usr/lib/x86_64-linux-gnu/libgstreamer-0.10.so.0.30.0

用apt-get來安裝尋找到的對應檔 installlibgstreamer0.10-0
sudo apt-get install libgstreamer0.10-0缺少libgstapp-0.10.so.0的方法同上
$apt-file search libgstapp-0.10.so.0

libgstreamer-plugins-base0.10-0: /usr/lib/x86_64-linux-gnu/libgstapp-0.10.so.0

libgstreamer-plugins-base0.10-0: /usr/lib/x86_64-linux-gnu/libgstapp-0.10.so.0.25.0

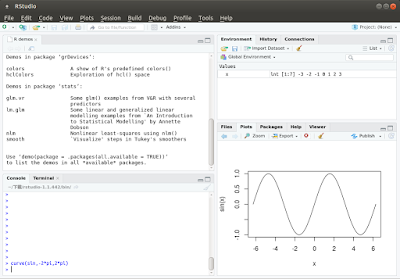
接著執行 ./rstudio 就可以有IDE整合環境了。 (如下圖)

以前學習R語言是沒有這環境的，為了提升開發效率才發展了這套工具，現在學生真的是蠻幸福的。

2018年3月18日星期日

春天的尾巴

新竹市東南街239巷沿著汀甫圳這一段的櫻花這幾年櫻花開得茂盛，只要盛開的時候總會吸引很多人前來拍照打卡，因此現在便成了著名的景點，又有人稱作櫻花巷。
粉嫩的景緻讓人不得不陶醉其中。

櫻花巷。富士櫻

Kodak Portra 800++ 濾鏡

LISP Programming 1062_ex2

exercise 2: improving the good-enough?
Refer to exercise 1.7

解答:
;exercise 2: improving the good-enough?
(define (average x y)
    (/ (+ x y) 2))
(define (improve guess x)
    (average guess (/ x guess))
)
(define (good-enough? old-guess new-guess)
    ;(> 0.01 (/ (abs (- new-guess old-guess)) old-guess))
    (< (/ (abs (- new-guess old-guess)) old-guess) 0.01)
)
(define (sqrt-iter guess x)
    (if (good-enough? guess (improve guess x)) ;調用新的good-enough?
        (improve guess x)
        (sqrt-iter (improve guess x) x)
    )
)
(define (sqrt x)
    (sqrt-iter 1.0 x))

執行結果：

2018年3月12日星期一

LISP Programming 1062_ex1

exercise 1: figure out the sum of squares of the minimum two arguments
Write a procedure named 'sum-of-square-min-two' which accepts three  
arguments and will figure out the sum of squares of the minimum two
arguments.

$ scheme48
> ,load ex1-sum-square-min-two.scm
> 
> (sum-of-square-min-two 1 2 3)
5
> (sum-of-square-min-two 1 2 -3)
10
> (sum-of-square-min-two 2 2 2)
8
> ,exit
$

解答:
;figure out the sum of squares of the minimum two arguments 
(define (square x)
      (* x x))
(define (min-two-square a b c)
    (if (<= a b)
        (if (<= b c)
            (list (square a) (square b))
            (list (square a) (square c)))
        (if (<= a c )
            (list (square b) (square a))
            (list (square b) (square c)))))
(define (sum-data x y)
    (+ x y))
(define (sum-of-square-min-two a b c)
    (apply sum-data (min-two-square a b c)))

執行結果：

認識Scheme

   兒子大二下學期程式設計選了一門"LISP程式設計"，這門課選用的語言是 Scheme，
是 LISP 的其中一個方言，應該對大多數人都蠻陌生的吧，因為它的確不是業界主流的程式
語言。老實說，我比較希望他能選一些Python或是Java的課程，畢竟將來是要靠這些"吃飯"的。

   剛剛有提到Scheme是LISP的方言，是1975年誕生於MIT人工智慧實驗室的一門程式語言。
那Scheme是一個怎麼樣的程式語言呢?
簡單來說Scheme是一種函數語言程式，意思是說，盡量把所有的函數都想成/寫成數學上的函數。
如果說Python 裡所有東西都是物件;那Scheme裡所有東西都是函數。

   約耳談軟體在2005年曾發表過一篇《The Perils of JavaSchools（爪哇學校的危害）》，
就談到不少 Java 不適合作為「First Programming Language」的問題，如果 Java 不適合
初學者，那有什麼更好的語言適合教學嗎？Joel Spolsky 的建議是 Scheme，這個主要用於
人工智慧領域的古老程式語言，Scheme 當時是 MIT 等多所名校 Computer Science 系所
的必修課程。而他們所使用的教材就是這本「SICP」。
(註:MIT 之所以從 SICP 轉換到現在的Python課程編制(2008)，是因為他們重新規劃了學習
的主軸。)

  「SICP」是 Structure and Interpretation of Computer Programs 的簡稱，又稱為

魔法書。是當年 MIT 赫赫有名的 6.001，是 EECS 的入門課，而這本書也影響了後續許多 CS 
的教材，甚至影響了很多以寫程式為工作或是以此為興趣的人，MIT電腦科學課程用這本書
當教材足足用了30年。

   相較於C/C++，Python 等等這些主流的語言，教材的資源也相當多，而台灣坊間Scheme 的
資源卻是少之又少，教授上課所用的Scheme 教材是SICP線上英文版，我找來找去發現對岸
的相關簡體書還蠻多的，就買了一本來看看。

為什麼這本書對於「CS 入門」來說具有革命性的意義? 主要有下面兩點：
.只專注一件事：計算的本質
.使用 Scheme 當作主要的語言

   通常，Computer Science 相關的入門課程，可能會花上很多時間在熟悉某個「程式語言」
上面，而不是去了解程式本身；又或者是有了大量的類比，來介紹電腦是個怎麼樣的東西；
但是 SICP 只專注一件事，那就是計算的本質這件事。

程式語言專家、大評論家王垠說：
    編程不過是一門失傳的藝術的別名，這門藝術的名字叫做"思考"。 —— 王垠

   兒子在剛上大學的時候我再三叮嚀他一定要把 C語言學好，因為 C語言學好了再學其他語言就
會非常容易好上手，學習不同語言其實就是換個思考方式來實作;
但如果以為學好C 就一定能學好Scheme嗎? 看看書中的內容比我想像中還要難尤其是遞迴
(Recursion)，我們常說"換了屁股就換了腦袋"，面對Scheme真的要換個思考(腦袋)方式才
能寫出優雅的程式。

既然這樣就好好的修這門課，試著用不同的思考方式來解決問題吧。

L. Peter Deutsch程式設計師說過一段經典名句:

"To iterate is human, to recurse, divine."

有人翻成:

"遞迴（recurse）只應天上有, 凡人該當用迴圈(iterate)"

2018年3月11日星期日

Ubuntu 忘記密碼的重置

有時候太多密碼是有可能忘記的，前幾天要使用一台安裝 Ubuntu 的筆電，由於太久沒有使用了竟然忘了登入密碼，如果Ubuntu忘記密碼無法登入怎麼辦? 下面是我的方法可以參考。

1. 首先用 LiveCD 開機，選擇 Try Ubuntu MATE

2. 開啟終端機，輸入 lsblk，看看目前磁碟的分割磁區有哪些，在這例子主要分割是 sda1

3. 接著輸入 sudo mount /dev/sda1 /mnt，將 sda1 掛載到 /mnt 目錄
然後輸入 sudo chroot /mnt，這時提示符號會成為 #
然後輸入 passed root ，更改 root 密碼
如果使用者密碼也需要更改就 passwd user-name

4. 輸入 sudo umount /mnt ，將 /mnt 目錄卸載，重新開機即可。

訂閱：文章 (Atom)

三葉草之家

網頁

2018年11月21日星期三

iTerm2 顯示/輸入中文

2018年10月10日星期三

Linux安裝套件出現“has no installation candidate”解決方式

2018年9月23日星期日

Virtual box guest additions: modprobe vboxsf failed

2018年7月14日星期六

真露燒酒

2018年6月25日星期一

我的西貢時光-越南滴滴壺

2018年6月4日星期一

LISP Programming 1062_ex9

2018年5月28日星期一

LISP Programming 1062_ex8

2018年5月21日星期一

LISP Programming 1062_ex7

2018年5月7日星期一

LISP Programming 1062_ex6

2018年4月30日星期一

LISP Programming 1062_ex5

【Scheme】連分法求Pi

2018年4月22日星期日

【Scheme】SICP Ex.1.37

2018年3月26日星期一

LISP Programming 1062_ex3

2018年3月22日星期四

無法連接iCloud解決方法

2018年3月21日星期三

Ubuntu 16.04 R語言安裝

2018年3月18日星期日

春天的尾巴

LISP Programming 1062_ex2

2018年3月12日星期一

LISP Programming 1062_ex1

認識Scheme

2018年3月11日星期日

Ubuntu 忘記密碼的重置

Python：台股ETF爬蟲(２)持股頁面

網頁

2018年11月21日 星期三

2018年10月10日 星期三

2018年9月23日 星期日

2018年7月14日 星期六

2018年6月25日 星期一

2018年6月4日 星期一

2018年5月28日 星期一

2018年5月21日 星期一

2018年5月7日 星期一

2018年4月30日 星期一

2018年4月22日 星期日

2018年3月26日 星期一

2018年3月22日 星期四

2018年3月21日 星期三

2018年3月18日 星期日

2018年3月12日 星期一

2018年3月11日 星期日

2018年11月21日星期三

2018年10月10日星期三

2018年9月23日星期日

2018年7月14日星期六

2018年6月25日星期一

2018年6月4日星期一

2018年5月28日星期一

2018年5月21日星期一

2018年5月7日星期一

2018年4月30日星期一

2018年4月22日星期日

2018年3月26日星期一

2018年3月22日星期四

2018年3月21日星期三

2018年3月18日星期日

2018年3月12日星期一

2018年3月11日星期日